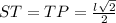Question

PQRS is a square and T is the intersection of he diagonals. STP=?

Answer 1

STP is a right, isosceles triangle.

The diagonals of a square cut the square itself in two equal right isosceles triangles. So, both diagonals cut the square in four right isosceles triangles.

STP is a right triangle because the two diagonal are perpendicular to each other, and it is isosceles because ST and TP are both half a diagonal, because the two diagonals intersect in their midpoint.

So, the angles of STP are 90, 45 and 45 degrees.

As for the lengths, SP is a side of the square, so let's call its length
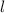`l`. The diagonals of a square are
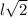`l√(2)` units long, and so
`ST = TP = (l√(2))/(2)`