Question

Jason inherited a piece of land from his great-uncle. Owners in the area claim that there is a 45% chance that the land has oil. Jason decides to test the land for oil. He buys a kit that claims to have an 80% accuracy rate of indicating oil in the soil. If the test predicts that there is no oil, what is the probability after the test that the land has oil? A. 0.1698 B. 0.2217 C. 0.5532 D. 0.7660

Answer 1

This is a Bayes Theorem Problem

P(oil | negative test) P(negative test)= P(negative test | oil) P(oil)

P(oil | negative test) = P(negative test | oil) P(oil) / P(negative test)

P(oil | negative test) =P(negative test | oil) P(oil) / ( P(negative test | oil) P(oil) + P(negative test | no oil) P(no oil) )

We're given the prior probability of oil, P(oil)=.45, so P(no oil)=.55

We given P(negative test | no oil) = 0.80, so P(negative test | oil) = .20

`P(\textrm{oil} | \textrm{negative test}) = ( .20(.45) )/(.20(.45) + .80(.55)) = 0.1698`

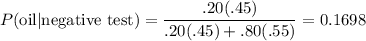
Choice A