Which of the following is the complete list of roots for the polynomial function f(x)= (x^2-2x-15)(x^2+8x+17) –5, 3 –5, 3, –4 + i, –4 – i –5, 3, –4 + i, 4 + i –4 + i, –4 – i

Question

asked Feb 24, 2019 86.4k views

2 Answers

Mmuller · Answer 1 · 2019-03-02T10:34:51+0000

Answer:

The complete set of roots is 5, -3, –4 + i, –4 – i

Explanation:

The given polynomial is

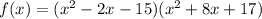
f(x)=(x^2-2x-15)(x^2+8x+17)

We equate to zero to get:

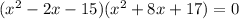
(x^2-2x-15)(x^2+8x+17)=0

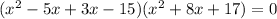
(x^2-5x+3x-15)(x^2+8x+17)=0

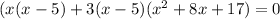
(x(x-5)+3(x-5)(x^2+8x+17)=0

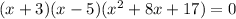
(x+3)(x-5)(x^2+8x+17)=0

This implies that:

x+3=0,or x-5=0 or
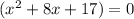
(x^2+8x+17)=0

x=-3,or x=5

For
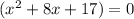(x^2+8x+17)=0 , we use the quadratic formula to get;

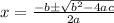
$x=(-b\pm√(b^2-4ac) )/(2a)$

where a=1,b=8,c=17

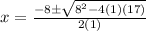
$x=(-8\pm√(8^2-4(1)(17)) )/(2(1))$

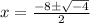
$x=(-8\pm√(-4) )/(2)$

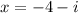x=-4-i or
x=-4+i

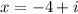
The complete solution is 5, -3, –4 + i, –4 – i