Answer:
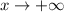 ,
,
 and
and
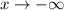 ,
,
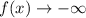 .
.
Explanation:
A polynomial is an algebraic function of the form:
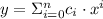 (1)
(1)
Where:
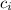 - i-th Coefficient.
- i-th Coefficient.
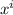 - i-th Power.
- i-th Power.
 - Grade of the polynomial.
- Grade of the polynomial.
 - Dependent variable.
- Dependent variable.
Mathematically speaking, polynomials are unbounded functions, and from graphic we notice that polynomial is of order 3 due to the fact that function pass through the x axis three times, where each point is a root of the polynomial.
Then, we may conclude that:
(i)
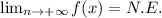
(ii)
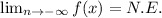
Then, the right answer is:
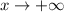 ,
,
 and
and
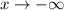 ,
,
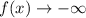 .
.