Question

Which row operation will trangularize this matrix?

Answer 1

`\left[\begin{array}{ccc}1&0&1\\0&0&1\\2&0&1\end{array}\right|\left\begin{array}{ccc}1\\6\\10\end{array}\right] \xrightarrow{-2R_1+R_3}\left[\begin{array}{ccc}1&0&1\\0&0&1\\0&0&-1\end{array}\right|\left\begin{array}{ccc}1\\6\\8\end{array}\right]\\\\Answer:\ C.\ -2R_1+R_3`

Answer 2

The correct option is C.

Explanation:

Triangular matrix is a square matrix in which either all the entries above the main diagonal or all the entries below the main diagonal are zero. These are now as upper triangular and lower triangular matrices respectively.

The given matrix is

`\begin{bmatrix}1 & 0 & 1|\ 1\\ 0 & 1 & 1|\ 6\\ 2 & 0 & 1 |10\end{bmatrix}`

In this matrix two elements below the main diagonal are zero. We need one more zero in first column of third row. So, we need to apply an operation to make a zero in first column of third row.

The element in first column of third row is 2.

The element in first column of first row is 1.

`R_3-2(R_1)=2-2(1)=0`

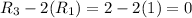
The required operation is
`-2R_1+R_3`.

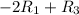Apply
`R_3\rightarrow -2R_1+R_3`,

`\begin{bmatrix}1 & 0 & 1|\ 1\\ 0 & 1 & 1|\ 6\\ 0 & 0 & -1 |\ 8\end{bmatrix}`

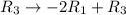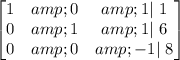
Therefore the correct option is C.