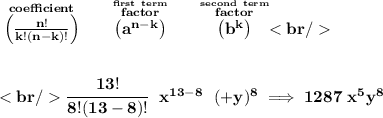Find the coefficient of x^5y^8 in (x+y)^13

Question

asked Dec 1, 2019 187k views

2 Answers

Sreepurna · Answer 1 · 2019-12-02T20:16:04+0000

recall that the exponent for the first term will be starting at 13, and descending by one on every expanded term, in the binomial theorem.

so, 13, 12, 11, 10, 9, 8, 7, 6, 5 <---- x⁵ will then be in the 9th term

now, using the "combination" formula to get the coefficient of the 9th term.

k = 8 <--- the 9th term

n = 13 <--- highest exponent

Robinvdvleuten · Answer 2 · 2019-12-05T22:50:46+0000

Binomial Theorem:

$(x+y)^n\quad=\quad\sum\limits_k^n\left(\begin{array}{cc}n\\k\end{array}\right) x^(n-k) y^k$

Where the coefficient is defined to be:

$\left(\begin{array}{cc}n\\k\end{array}\right)\quad=\quad (n!)/(k!(n-k)!)$

Notice that the exponent on y is 8 for the term they gave us.

This is the term which corresponds to k=8.

$\left(\begin{array}{cc}13\\8\end{array}\right)x^(13-8)y^8$

So our coefficient is:

$\left(\begin{array}{cc}13\\8\end{array}\right)\quad=\quad(13!)/(8!(13-8)!)$

If you expand the factorial in the numerator,

you can cancel some stuff out,

$(13\cdot12\cdot11\cdot10\cdot9\cdot8!)/(8!\cdot5!)\quad=\quad (13\cdot12\cdot11\cdot10\cdot9)/(5!)$

Further simplification should get you to this:

$13\cdot11\cdot3\cdot3\quad=\quad1287$