Question

Geometry! Please help!

This composite shape has an area of 136 cm².

What is the height of the trapezoid?



Enter your answer in the box.

Answer 1

4 cm.

Explanation:

We have been given that the given composite figure has an area of 136 square cm.

First of all let us find the area of trapezoid by subtracting the area of rectangle from the area of composite figure.

`\text{Area of rectangle}=\text{Length*Width}`

`\text{Area of rectangle}=\text{6 cm*14 cm}`

`\text{Area of rectangle}=84\text{ cm}^2`

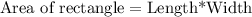
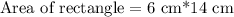
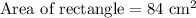
So the area of rectangle is 84 square cm.

`\text{Area of trapezoid}=136\text{ cm}^2-84\text{ cm}^2`

`\text{Area of trapezoid}=52\text{ cm}^2`

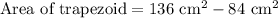
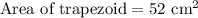
We will use area of trapezoid formula to solve for the height of our given trapezoid.

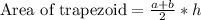`\text{Area of trapezoid}=(a+b)/(2)*h`, where a and b represents lengths of parallel bases and h represents height of trapezoid.

Upon substituting our given values in above formula we will get,

`52\text{ cm}^2=\frac{\text{12 cm+14 cm}}{2}*h`

`52\text{ cm}^2=\frac{\text{26 cm}}{2}*h`

`52\text{ cm}^2=13\text{ cm}*h`

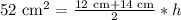
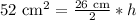
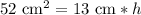
Let us divide both sides of our equation by 13 cm.

`\frac{52\text{ cm}^2}{13\text{ cm}}=\frac{13\text{ cm}*h}{13\text{ cm}}`

`4\text{ cm}=h`

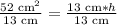
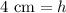
Therefore, height of our given trapezoid is 4 cm.