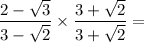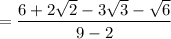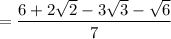Question

90 POINTS!!! HELP. How do you simplify: (2 - the square root of 3) / (3 - the square root of 2)

Answer 1

`(2 - √(3))/(3 - √(2))`

What you need to do is to rationalize the denominator.
You are not supposed to leave a root in the denominator,
so you need to change the form of this fraction so that there
is no root in the denominator.

The process to do this is calling "rationalizing the denominator."
You will end up with an integer in the denominator.


`(2 - √(3))/(3 - √(2)) * (3 + √(2))/(3 + √(2))=`


`= ((2 - √(3))(3 + √(2)))/((3 - √(2))(3 + √(2)))`


`= (6 + 2 √(2) - 3 √(3) - √(6))/(9 - 2)`


`= (6 + 2 √(2) - 3 √(3) - √(6))/(7)`

Answer 2

You can simplify this by rationalizing the denominator. One does this by multiplying by the conjugate of the quantity in the denominator (this rationalizes it).


`(2- √(3) )/(3- √(2) )`=

=
`(2- √(3) )/(3- √(2) )` *
`(3+ √(2) )/(3+ √(2) )`

Now, the final step is to carry out the multiplication for the denominator. The final answer becomes:


`((2- √(3))(3+ √(2)) )/(7)`