Question

60 POINTS, please help me with trig.

Answer 1

First problem: draw a line segment through the vertex R and a point C on PQ such that the segment is perpendicular to PQ, thus forming an altitude of the triangle. This new segment CR, the new segment CP, and PR form a 30-60-90 right triangle, where the measure of angle PCR is 90 degrees. CR then occurs with PR in a ratio of
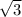
`\sqrt3` to 2, so


`(CR)/(PR)=\frac{CR}5=\frac{\sqrt3}2\implies CR=\frac{5\sqrt3}2`

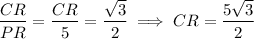
and this can be considered the height of a triangle whose base is PQ. The area is then


`\frac12\cdot6\cdot\frac{5\sqrt3}2=\frac{15\sqrt3}2\approx13`

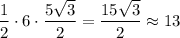
Second problem: the sum of the interior angles of any triangle is 180, so the measure of the missing angle must be 180 - 20 - 35 = 125 degrees. By the law of sines, the length of the missing side (call it
`x`) satisfies


`\frac{\sin20^\circ}9=\frac{\sin125^\circ}x\implies x\approx21.56`

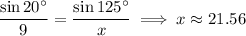
Use Heron's formula to find the area of the triangle:


`A=√(s(s-a)(s-b)(s-c))`

where
`A` is the area,
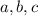
`a,b,c` are the lengths of the sides, and
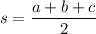
`s=\frac{a+b+c}2` is the half the perimeter of the triangle. Then the area is about
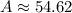
`A\approx54.62` square feet. Convert to square yards:


`54.62\text{ ft}^2\cdot\left(\frac{1\text{ yd}}{3\text{ ft}}\right)^2\approx6.07\text{ yd}^2`

then round up to 7 square yards. At a price of $12.50 per square yard, the total price will be $87.50.