Question

The coordinates of rhombus ABCD are A(–4, –2), B(–2, 6), C(6, 8), and D(4, 0). What is the area of the rhombus? Round to the nearest whole number, if necessary. 30 square units 60 square units 102 square units 120 square units

Answer 1

Hello !
If you mist find the area of the rhombus,you need to calculate the length of the diagonals.

We have the rhombus ABCD.The diagonals are are AC and BD .
Here's a formula to find out the distance between two points in the Cartesian system : (let's take randomly 2 point and their coordinates)

M (m₁,m₂) ; N (n₁,n₂) ⇒ MN = \sqrt{ (m_{1} - n_{1})^{2} + (m_{2} - n_{2})^{2} }


Now it's simple to calculate the diagonals :


`AC = \sqrt{ (-4-6)^(2) +(-2-8)^(2)} \\ \\ AC= \sqrt{ (-10)^(2) + (-10)^(2) } \\\\AC = √( 100+100) \\\\ AC =√( 200 ) \\\\AC=10 √(2) \\ \\ \\ BD = \sqrt{ (-2-4)^(2) + 6^(2) } \\\\BD=\sqrt{ (-6)^(2) + 6^(2) }\\\\BD= \sqrt{6^(2)+6^(2)} \\\\BD= √(36+36) \\\\BD= √(72) \\\\BD=6 √(2)`



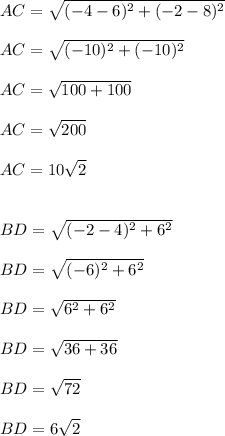
The area is :
`(AC*BD)/(2) = ( 10√(2) * 6√(2) )/(2) = (60*2)/(2) =60`


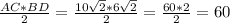
Answer: 60 u²



The representation is below.
Have a nice day :)