Which of the following shows both the boundary lines to the solution of the inequality lx+3l-2\leq 0, and a value that is included in the region which determines the solution? x…

Question

Which of the following shows both the boundary lines to the solution of the inequality lx+3l-2
`\leq` 0, and a value that is included in the region which determines the solution?

x = 0

x = –1

x = 2

x = 5

Answer 1

Solving this inequality will yield the answer

`|x+3|\leq 2`

`\left \{ {{x+3 \leq 2} \atop {x+3 \geq -2}} \right.`

`\left \{ {{x \leq -1} \atop {x \geq -5}} \right.`

-1 is located on the border and it is the correct answer from these below given multiple choices.

Answer 2

Answer: x = –1

Explanation:

Given inequality:
`|x+3|-2 \leq0`

When we simplify the above inequality we get,

`|x+3|\leq2\\\\\Rightarrow-2\leq(x+3)\leq2\\\\\Rightarrow-2-3\leq x\leq2-3\\\\\Rightarrow-5\leq x\leq -1`

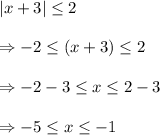
From all the given options only -1 t is included in the region [-1,-5].

Hence, x = –1 is the value that is included in the region which determines the solution.