Hi there!
• f(6) = (0.25 × 6 - 0.5) × 6 + 3.5 = 9.5
• f(2) = (0.25 × 2 - 0.5) × 2 × 3.5 = 3.5
Th' average rate of change (m) is the ratio of th' change in function value w.r.t width of the Interval.
Acc'rding to rhe question :-
m =

m =
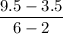
m =

=

= 1.5
Hence,
The required answer is 1.5 thousand owners per year.
~ Hope it helps!