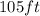1. Identify the parallelogram as
 .
.
2. The diagonal divides it into two congruent triangles, so let's take only the triangle
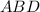 , where
, where
 is the diagonal.
is the diagonal.
3. Now, you must apply the Law of Cosines:

Where
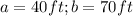 and
and
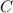 is the angle between
is the angle between
 and
and
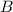 .
.
4.
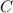 and
and
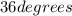 are suplementary. Therefore:
are suplementary. Therefore:

5. Substitute values into the formula:
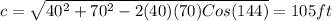
The answer is: