Question

Suppose p(a) = 0.40 and p(a 

b.= 0.55. find p(b) if …
a.… p(a 
b.= 0.30;
b.… p(a 
b.= 0.45;
c.… a and b are mutually exclusive;
d.… a and b are independent.

Answer 1

Between the probability of union and intersection, it's not clear what you're supposed to compute. (I would guess it's the probability of union.) But we do know that


`P(A\cup B)+P(A\cap B)=P(A)+P(B)`


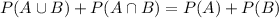
For parts (a) and (b), you're given everything you need to determine
`P(B)`.

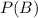
For part (c), if
`A` and
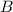
`B` are mutually exclusive, then
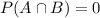
`P(A\cap B)=0`, so
`P(A\cup B)=P(A)+P(B)`. If the given probability is
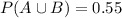
`P(A\cup B)=0.55`, then you can find
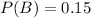
`P(B)=0.15`. But if this given probability is for the intersection, finding
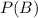
`P(B)` is impossible.


For part (d), if
`A` and
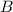
`B` are independent, then
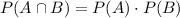
`P(A\cap B)=P(A)\cdot P(B)`.