In order to find any of the info they want, we first have to find the first derivative. This will give us the slope formula we need to eventually find the equation of the line tangent at that point (1, 7). The first derivative is
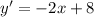
. Subbing in the x value from the point, we get y' = -2(1)+8. That means that the slope is 6 at that point. Using that x and y value from the point along with that slope in the slope-intercept form of a line, we can solve for b. 7=6(1)+b and b = 1. The equation for the line tangent to that parabola at that point is y = 6x + 1.