Question

Find the value of x such that 3^(x^2)/ (3^(2x))=27

Answer 1

This is how this one is done. I'm assuming by this type of a problem that you are in logs in math since you need to rules of logs to solve it. First things first...laws of exponents when the bases are like. Our base is a 3. Here's the problem written out:
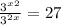
`(3^ x^(2) )/(3 ^(2x) ) =27`. The rules for exponents when dividing like bases is that you subtract the exponents. So we will do that:
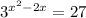
`3^(x^2-2x) =27`. Since we are solving for x we need to find a way to get it down from its exponential position. We do that by takking the log of both sides.
`log 3^(x^2-2x)=log27`. Another rule of logs, the power rule, is that once we take the log of a base with an exponent, we can move the exponent down in front, like this:
`x^2-2x[log(3)]=log27`. Now we will divide both sides by log(3) to get
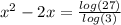
`x^2-2x= (log(27))/(log(3))`. We do that math on the right side on our calculator to get
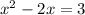
`x^2-2x=3`. Now this is something we can handle. We have a second degree polynomial that we have to factor for x. Do that by moving the 3 over by subtraction.
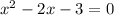
`x^2-2x-3=0`. Factoring that you have that x = 3 and x = -1. There you go!