Question

The expression sinx(cscx-cotx cosx) can be simplified to

Answer 1

sin x and csc x are reciprocals, so sin x ( csc x) = 1.

Next:

sin x -cos x
------ * ----------- * cos x = - (cos x)^2
1 sin x

Then we have 1 - (cos x)^2, which in turn is equal to (sin x)^2 (answer)

Answer 2

The expression sinx(cscx-cotx cosx) can be simplified to sin²x.

Explanation:

Consider the provided trigonometric expression.

`sinx(cscx-cotx cosx)`

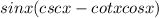
Open the parentheses and apply the distributive property: a(b+c)=ab+ac

`sinx\cdot cscx-cotx \cdot cosx \cdot sinx`

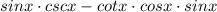
Now use the identity:
`cscx= (1)/(sinx), cotx=(cosx)/(sinx)`

`sinx\cdot (1)/(sinx)-(cosx)/(sinx) \cdot cosx \cdot sinx`

`1-cos^2x`

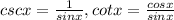
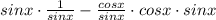
Use the identity: 1 - cos²x = sin²x

Thus,
`1-cos^2x=sin^2x`

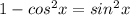
Hence the expression sinx(cscx-cotx cosx) can be simplified to sin²x.