Question

Derive the equation of the parabola with a focus at (0, −4) and a directrix of y = 4.

f(x) = −16x2

f(x) = 16x2

f(x) = − one sixteenth x2

f(x) = one sixteenth x2

Answer 1

the answer is -1/16 x^2

which is C

Explanation:

have a good day

Answer 2

The statement above is represented in the figure below. We have plotted the focus, the directrix and the parabola. So we know that the parabola opens downward. We also know that:


`\left | \overline{FV} \right |=\left | \overline{VA} \right |=4 \ \ then \ the \ vertex \ is: \\ \\ V(0,0)`

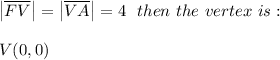
Because this is true the equation of the parabola is:


`x^2=4py`

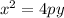
So our goal is to find the value of
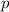
`p`. Given that the parabola opens downward, then
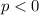
`p<0` and from the figure:


`F(0,p)=(0,-4) \\ \\ \therefore p=-4`

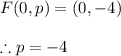
Accordingly:


`x^2=4(-4)y \\ \\ \therefore \boxed{y=-(1)/(16)x^2}`

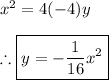
Finally, the right answer is f(x) = − one sixteenth x2