Question

When 92/3 is written in simplest radical form, which value remains under the radical?

Answer 1

We know that 9²/3 is the cube root of 9².
When we factor, we get 3 as the radical.

So your Answer is = 3

Answer 2

`3\sqrt[3]{3}`; 3 will remain under radical.

Explanation:

We have been given a number
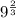`9^{(2)/(3)}`. We are asked to write our given number in simplest radical form.

Using exponent property for radicals
`a^{(m)/(n)}=\sqrt[n]{x^m}`, we can rewrite our expression as:

`9^{(2)/(3)}=\sqrt[3]{9^2}`

`9^{(2)/(3)}=\sqrt[3]{81}`

`9^{(2)/(3)}=\sqrt[3]{27*3}`

`9^{(2)/(3)}=\sqrt[3]{3^3*3}`

Pulling out 3 from radical, we will get:

`9^{(2)/(3)}=3\sqrt[3]{3}`

Therefore, the simplest form of our given expression would be
`3\sqrt[3]{3}` and 3 will remain under radical.