Question

Explain how to find the exact value of sec 13pi/4, including quadrant location.

Answer 1

First of all, let's convert this angle from radians to degree, so applying rule of three:


`\pi \ radians ---\ \textgreater \ 180^(\circ) \\ (13\pi)/(4) \ radians --\ \textgreater \ x \\ \\ x=(13\pi)/(4)* (180)/(\pi)=585^(\circ)`

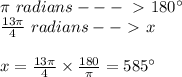
So we can represent this angle as follows:


`585^(\circ)=360^(\circ)+225^(\circ)`

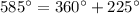
One complete turn equals 360°, so if a point is traveling in a circumference, the position of the point in 585° is the same as in the angle of 225°. In this way, we also know the following regarding quadrants:


`Let \ x:An \ angle \\ \\ 0^(\circ) \ \textless \ x \ \textless \ 90^(\circ) \ I \ Quadrant \\ 90^(\circ) \ \textless \ x \ \textless \ 180^(\circ) \ II \ Quadrant \\ 180^(\circ) \ \textless \ x \ \textless \ 270^(\circ) \ III \ Quadrant \\ 270^(\circ) \ \textless \ x \ \textless \ 360^(\circ) \ IV \ Quadrant`

Given that 225° is between 180° and 270° then the conclusion is that this angle is in the III Quadrant and we can find the value as follows:


`sec((13\pi)/(4))=sec(585^(\circ))=sec(225^(\circ))= (1)/(cos(225^(\circ)))=- √(2)`