Question

If ABCD ≅ QRST, m∠A = x - 10, and m∠Q = 2x - 30, what is m∠A?

Answer 1

If ABCD ≅ QRST, then m∠A = m∠Q,
so
x-10 = 2x - 30
2x-x=30-10
x=20

m∠A = x - 10 =20-10 = 10
m∠A = 10⁰

Answer 2

`m\angle A = 10^\circ`

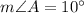
Explanation:

We are given the following information in the question:

`ABCD \cong QRST\\m\angle A = x -10\\m\angle Q = 2x-30`

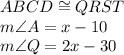
Since,quadrilateral ABCD is congruent to the quadrilateral QRST, then by the property of congruency, we can write,

`m\angle A = m\angle Q`

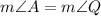
Equating the value of the two angles, we get,

`m\angle A = m\angle Q\\x - 10 = 2x - 30\\2x - x = 30-10\\x = 20`

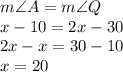
Putting the value of x to obtain measure of angle A.

`m\angle A = x -10 = 20-10\\m\angle A = 10^\circ`

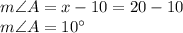
Thus, the measure of angle A is 10 degrees.