Question

8 when volleyballs are purchased, they are not fully inflated. a partially inflated volleyball can be modeled by a sphere whose volume is approximately 180 in3. after being fully inflated, its volume is approximately 294 in3. to the nearest tenth of an inch, how much does the radius increase when the volleyball is fully inflated

Answer 1

The volume of the sphere by definition is:

`V = (4/3) \pi * r ^ 3`
Clearing the radio we have:

`r = \sqrt[3]{ (3V)/(4 \pi)}`
For the initial condition we have that the radius is:

`r1 = \sqrt[3]{ (3(180))/(4 \pi)}`

`r1 = 3.50`
For the final condition we have that the radius is:

`r1 = \sqrt[3]{ (3(294))/(4 \pi)}`

`r1 = 4.12`
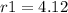
Then, the difference between both values is given by:

`r2 - r1 = 4.12 - 3.50 r2 - r1 = 0.62 in`
Answer:
the radius increase 0.62 inches when the volleyball is fully inflated