Question

How many solutions does this linear system have?

y = 2x – 5

–8x – 4y = –20

Answer 1

the second one would be y=-2x+5, and it would only have one solution.

solution is (2.5, 0)

Answer 2

Explanation:

Equations
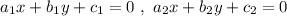`a_1x+b_1y+c_1=0\,\,,\,\,a_2x+b_2y+c_2=0` have

1.unique solution if
`(a_1)/(a_2)\\eq (b_1)/(b_2)`

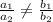
2. infinite solutions if
`(a_1)/(a_2)= (b_1)/(b_2)=(c_1)/(c_2)`

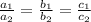
3. no solution if
`(a_1)/(a_2)= (b_1)/(b_2)\\eq (c_1)/(c_2)`

We can write equations:
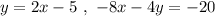`y=2x-5\,\,,\,\,-8x-4y=-20` as follows:

`2x-y-5=0\,\,,\,\,-8x-4y+20=0`

On comparing these equations with standard equations
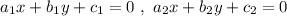`a_1x+b_1y+c_1=0\,\,,\,\,a_2x+b_2y+c_2=0` , we get
`a_1=2\,,b_1=-1\,,\,c_1=-5\,,a_2=-8\,,b_2=-4\,,c_2=20`

such that

`(a_1)/(a_2)=(2)/(-8)=(-1)/(4)\\(b_1)/(b_2)=(-1)/(-4)=(1)/(4)\\(c_1)/(c_2)=(-5)/(20)=(-1)/(4)`

Here,
`(-1)/(4)=(a_1)/(a_2)\\eq (b_1)/(b_2)=(1)/(4)`

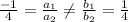
So, according to the facts explained above,

The given linear system has a unique solution i.e only one solution.