Question

HELP WITH CALCULUS

Find the area bounded by the curve y = x^2 and the straight line y = 2 + x.
A. 4 1/2
B. 4 1/6
C. 5 1/2
D. 5 1/6

Answer 1

A. 4 1/2

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Functions

• Function Notation
• Graphing

Solving systems of equations by graphing

Calculus

Integration

• Integrals
• Definite Integrals
• Integration Constant C
• Area under the curve

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

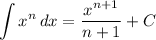
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

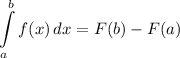
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

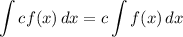
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

Step 1: Define

y = x²

y = 2 + x

Step 2: Identify

See Attachment. Find other necessary information.

Interval [-1, 2]

Step 3: Find Area

1. Substitute in variables [Area of a Region Formula]:
   `\displaystyle A = \int\limits^2_(-1) {(2 + x - x^2)} \, dx`
2. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle A = \int\limits^2_(-1) {2} \, dx + \int\limits^2_(-1) {x} \, dx - \int\limits^2_(-1) x^2} \, dx`
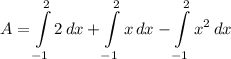
3. [1st Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle A = 2\int\limits^2_(-1) {} \, dx + \int\limits^2_(-1) {x} \, dx - \int\limits^2_(-1) x^2} \, dx`
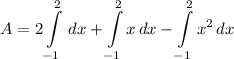
4. [Integrals] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = 2(x) \bigg| \limits^2_(-1) + (x^2)/(2) \bigg| \limits^2_(-1) - (x^3)/(3) \bigg| \limits^2_(-1)`
5. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle A = 2(3) + (3)/(2) - 3`
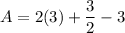
6. Simplify:
   `\displaystyle A = (9)/(2)`
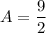
7. Reduce:
   `\displaystyle A = 4(1)/(2)`

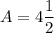
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e