Answer:
Option 3 rd is correct
sum of the given geometric series is, 40
Explanation:
The sum of the finite geometric series is given by:

 ....[1]
....[1]
Given that:
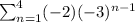
We have to find the
 for the series:
for the series:


here,
 and common ratio(r) = -3
and common ratio(r) = -3
Substitute these in [1] we have;

⇒

⇒

Simplify:

therefore, the sum of the given geometric series is, 40