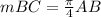Question

Can someone answer these as well worth lots of points. Only Appropriate Answers Pls :).

Answer 1

1. To solve this we are going to find the distance of the three sides of each triangle, and then, we are going to use Heron's formula.
- For triangle RTS:
S (2,1), T (1,3) and R (5,5). Using a graphic tool or the distance formula
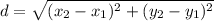
`d= \sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}` we realize that ST=2.2, SR=5, and TR=4.5. Now we are going to find the semi-perimeter of our triangle:

`s= (ST+SR+TR)/(2)`

`s= (2.2+5+4.5)/(2)`

`s= (11.7)/(2)`

`s=5.85`
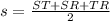
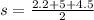
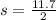
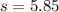
Now we can use Heron's formula:

`A= √(s(s-ST)(s-SR)(s-TR))`

`A= √(5.85(5.85-2.2)(5.85-5)(5.85-4.5))`

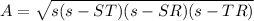
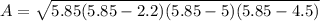
`A=4.9` square units
We can conclude that the area of triangle RTS is 4.9 square units.

- For triangle MNL:
M (2,-4), N (-2,-3), and L (0,-1). Once again, using a graphic tool or the distance formula we get that MN=4.1, ML=3.6, and NL=2.8.
Lets find the semi-perimeter of our triangle to use Heron's formula:

`s= (4.1+3.6+2.8)/(2)`

`s=5.25`

`A= √(5.25(5.25-4.1)(5.25-3.6)(5.25-2.8))`

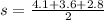
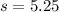
`A=4.9` square units
We can conclude that the area of triangle MNL is 4.9 square units.

2. To find the volume of our pyramid, we are going to use the formula for the volume of a rectangular pyramid:
`V= (lwh)/(3)`
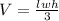
where

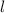
`l` is the length of the rectangular base

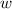
`w` is the width of the rectangular base

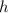
`h` is the height of the pyramid
From our picture we can infer that
`l=15`,
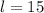
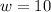
`w=10`, and
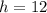
`h=12`, so lets replace the values in our formula:

`V= (lwh)/(3)`

`V= ((15)(10)(12))/(3)`

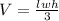
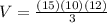
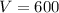
`V=600` cubic units

To find the volume of the cone, we are going to use the formula:
`V= \pi r^2 (h)/(3)`
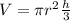
where

`r` is the radius

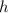
`h` is the height
From our picture we can infer that the diameter of the cone is 9; since radius is half the diameter,
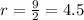
`r= (9)/(2) =4.5`. We also know that
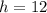
`h=12`, so lets replace the values:

`V= \pi r^2 (h)/(3)`

`V= \pi (4.5)^2 (12)/(3)`

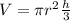
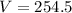
`V=254.5` cubic units
We can conclude that the volume of the pyramid is 600 cubic units and the volume of the cone is 254.5 cubic units

3. To find
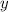
`y`, we are going to use the tangent trigonometric function:

`tan( \alpha )= (opposite.side)/(adjacent.side)`

`tan(53)= (4cm)/(y)`

`y= (4cm)/(tan(53))`

`y=3.01cm`
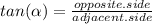
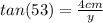
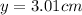
and to the nearest whole number:

`y=3cm`
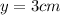
We can conclude that
`y=3cm`

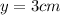4. To solve this, we are going to find the volume of the cube first; to do it we are going to use the formula for the volume of a cube:
`V=a^3`
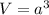
where

`a` is the edge of the cube
Since the sphere fits exactly in the cube, the edge of the cube is equal to the diameter of the sphere; therefore,
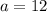
`a=12`. Lets replace the value in our formula:

`V=(12)^3`

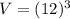
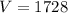
`V=1728` cubic units
Next, we are going to use the formula for the volume of a sphere:
`V= (4)/(3) \pi r^3`
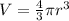
where

`r` is the radius of the sphere
We know form our problem that the diameter of the sphere is 12 units, since radius is half the diameter,
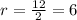
`r= (12)/(2) =6`. Lest replace the value in our formula:

`V= (4)/(3) \pi r^3`

`V= (4)/(3) \pi (6)^3`

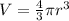
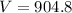
`V=904.8` cubic units
Now, to find the volume of the empty space in the cube, we just need to subtract the volume of the sphere form the volume of the cube:

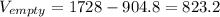
`V_(empty)=1728-904.8=823.2` cubic units
We can conclude that the volume of the empty space in the cube is 823.2 cubic units

4. To solve this, we are going to use the arc length formula:
`s= ( \alpha)/(360) 2 \pi r`
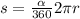
where

`s`=mBC

`s` is the length of the arc

`r` is the radius of the circle
Lets, find
`x` first. From the picture we can infer that:

`x+2x+x=180`

`4x=180`

`x= (180)/(4)`

`x=45`
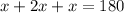
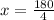
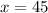
Since BE is the diameter of the circle, AB is its radius; therefore
`r=AB`. Lets replace the values in our formula:

`s= ( \alpha)/(360) 2 \pi r`

`s= (45)/(360) 2 \pi AB`

`s= ( \pi )/(4) AB`

`mBC= ( \pi )/(4) AB`
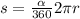
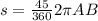
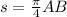
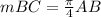We can conclude that
`mBC= ( \pi )/(4) AB`