Question

Type the correct answer in the Box use numerals instead of words if necessary use / for the fraction bar find the missing term

The roots of x^2-(answer)+34 are 5+- 3i

Answer 1

The roots of the given equation are 5 + 3i, 5 - 3i.

This means the two factors of the given polynomial are x - (5+3i) and x - (5 - 3i). The product of the factors must result in the original expression. So, we can write:

x² - (answer) + 34 = (x - 5 -3i)(x - 5 + 3i) (Equation 1)

Simplifying the right hand side:


`(x - 5 -3i)(x - 5 + 3i) \\ \\ = x^(2) -5x+3xi-5x+25-15i-3xi+15i-9i^(2) \\ \\ = x^(2) -10x+25-9i^(2) \\ \\ = x^(2) -10x+25-9(-1) \\ \\ = x^(2) -10x+25+9 \\ \\ = x^(2) -10x+34`

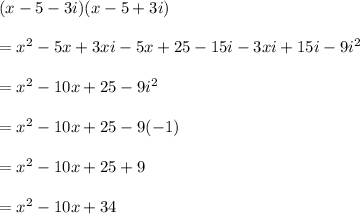
Thus, we can write the Equation 1 as:

x² - (answer) + 34 = x² - 10x + 34

Comparing the two sides, we can conclude that the answer to this question is 10x.