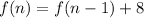Answer:
The first term is 3 and common difference is 8.
And
The formula for sequence is:
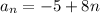
Function is:
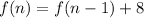
Explanation:
Given that
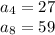
The general formula for arithmetic sequence is:
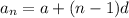
Here
a is the first term
n is the term number
and d is the common difference
for 4th term
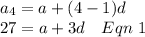
For 8th term
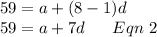
subtracting equation 1 from equation 2
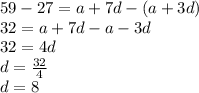
Putting d = 8 in equation 1
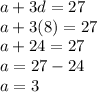
Now for the function
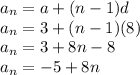
The sequence can also be expressed as a function as:
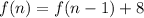
Hence,
The first term is 3 and common difference is 8.
And
The formula for sequence is:
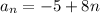
Function is: