Question

Find condition that zeros of polynomial p(x)=ax2+bx+c are reciprocal of each other

Answer 1

Suppose
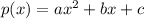
`p(x)=ax^2+bx+c` has two roots, reciprocals of one another. Call them
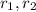
`r_1,r_2`, with
`r_2=\frac1{r_1}`.

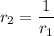
Let's divide through
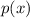
`p(x)` by
`a` for now. By the fundamental theorem of algebra, we can factorize
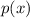
`p(x)` as


`x^2+\frac ba x+\frac ca=(x-r_1)(x-r_2)=(x-r_1)\left(x-\frac1{r_1}\right)`

Expand the RHS to get


`x^2-\left(r_1+\frac1{r_1}\right)x+1`

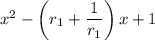
so we must have


`-\frac ba=r_1+\frac1{r_1}`

`\frac ca=1`

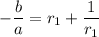
The first equation says
`a` and
`b` occur in a ratio of the negative sum of the roots of
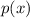
`p(x)`, while the third equation says that the first and last coefficients
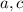
`a,c` must be the same.