How do you find the limit of # (3 x^4 + 4) / ((x^2 - 7)(4 x^2 - 1)) # as x approaches infinity?

Question

asked Dec 14, 2019 186k views

1 Answer

Nikolay Prokopyev · Answer 1 · 2019-12-18T15:34:36+0000

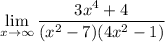
$\displaystyle\lim_(x\to\infty)(3x^4+4)/((x^2-7)(4x^2-1))$

Expanding the denominator gives

(x^2-7)(4x^2-1)=4x^4-29x^2+7

Then in the whole rational expression, we can divide through by
x^4

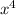
. Since
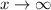
$x\to\infty$ , we assume that
x>0

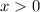
, so this is legal.

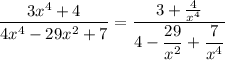
$(3x^4+4)/(4x^4-29x^2+7)=\frac{3+\frac4{x^4}}{4-(29)/(x^2)+\frac7{x^4}}$

As

gets arbitrarily large, the rational terms in the numerator and denominator become negligible. So for large

, we have

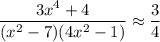
$(3x^4+4)/((x^2-7)(4x^2-1))\approx\frac34$

And so the limit is
$\frac34$ .