Answer:
It takes
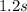 to hit the ground.
to hit the ground.
Explanation:
We have the following function that models the situation :
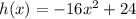
Where ''h'' represents the height in feet and ''x'' represents the time in seconds.
When the sunglasses hits the ground, its height is
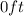 .
.
We can replace
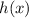 by
by
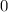 and calculate the value of ''x'' that verifies the expression (its unit will be seconds) ⇒
and calculate the value of ''x'' that verifies the expression (its unit will be seconds) ⇒
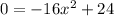
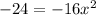
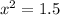
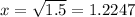 (We know that
(We know that
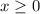 because a negative value of time is absurd)
because a negative value of time is absurd)
1.2247 rounded to the nearest tenth is 1.2
Finally, we found out that the sunglasses will hit the ground in
 seconds.
seconds.