Question

The grades on the last math exam had a mean of 72%. Assume the population of grades on math exams is known to be distributed normally, with a standard deviation of 5%. Approximately what percent of students earn a score between 72% and 87%? please explain each step.

Answer 1

The exam scores are distributed normally with mean 72 and standard deviation 5.
Recall the empirical (68 - 95 - 99.7) rule, which says that approximately 95% of a normal distribution lies within two standard deviations of the mean. Put another way,


`\mathbb P(|S-72|\le2\cdot5)=\mathbb P(-10\le S-72\le10)=\mathbb P(62\le S\le87)\approx0.95`


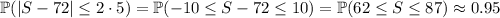
Also recall that the normal distribution is symmetric about its mean. This means that


`\mathbb P(|S-72|\le 5)=2\,\mathbb P(0\le S-72\le 5)=2\,\mathbb P(72\le S\le77)\approx0.95`

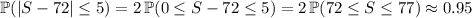
From this last equation, it follows that


`\mathbb P(72\le S\le 77)\approx\frac{0.95}2=0.475=47.5\%`

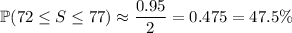
That is, about 47.5% of the students scored between 72 and 87 on the exam.