Question

Write the integral in one variable to find the volume of the solid obtained by rotating the first-quadrant region bounded by y = 0.5x^2 and y = x about the line x = 3.

Answer 1

A graph can be helpful for finding limits of integration.

The volume can be found using cylindrical shells of height (x-0.5x^2) and radius (3-x).

`V=\int\limits_(0)^(2){2\pi (3-x)(x-0.5x^(2))}\,dx`

_____
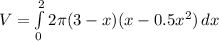
The parabola whose area is shaded purple is the difference between the curves y=x and y=0.5x^2. The area under the parabola shaded purple is
(2/3)*height*width = (2/3)*(0.5)*2 = 2/3
The volume is that area multiplied by the circumference of the circle about which its centroid is revolved. That circle has radius 2, so its circumference is 4π. Then the volume is
V = (2/3)*4π = 8π/3