Answer:
0.1056
Explanation:
A large company claims that the average age of their employees is 32 years i.e.
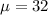
Standard deviation =
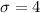
The average age of employees in the sales department at the company is 27 years i.e.
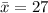
The z-score corresponding to x = 27 is calculated as:
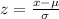 ,
,
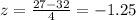
Now, From a z-table,
The probability that x < 27 corresponds to the probability that z < -1.25:
P(z < -1.25) = 0.1056
Hence the probability that an employee, chosen at random, will be younger than 27 years is 0.1056