Question

Re the graphs of the lines in the pair parallel? Explain. y = 3/7x + 11 –3x + 7y = 13

Answer 1

To the pair be parallel, it must meet the (Mr = Ms) rule, Slope of the R line = Slope of the S line.

*The letters used to refer the lines could be any

I will designate the first line equation as "R" and the second "S".

`r: \: y = (3x / 7) + 11 \\ s: \: - 3x + 7y = 13`

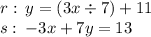
Now we have to adjust the "S" line to the Slope-Intercept form:

`y = mx + n`

`s: \: y = 3x + 13 / 7`

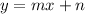
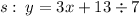
To see better which is each term, i will make another little adjust:

`s: \: y = (3x / 7) + (13 / 7)`

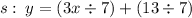
I will let the "R" line here too to view.

`r: \: y = (3x / 7) + 11`

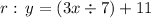
Now we have to identify which terms are the Slopes (Mr, Ms) of the equations:

y = mx + n

-> s: y = 3x/7 + 11
-> Ms = 3/7 ; Ns = 11

-> r: y = 3x/7 + 13/7
-> Mr = 3/7 ; Nr = 13/7

Now see if they meet the condition (Mr = Ms):

3/7 = 3/7

Answer: The pair is parallel because the Slope of each line has the same value.