Question

The two triangular prisms shown are similar. The dimensions of the larger prism were multiplied by a scale factor of to create the smaller prism.

When the large prism was reduced, the surface area changed by a factor of
A.64/125
B.16/25
C.4/5
D.10/8

Answer 1

16/25 is going to be your answer. Just took the test and got 100

Answer 2

Answer: B.
`(16)/(25)`

Explanation:

We know that if a figure or solid shape is dilated to create a new shape then the new shape is similar to the original shape.

Also, the scale factor of dilation is the ratio of the sides of new shape to the corresponding sides of the original shape .

Let k be the scale factor of dilation, then

Given : Original shape - larger prism

New shape - smaller prism

Surface area of prism with all sides equal (a)=
`4a^2`

Surface area of original prism =
`4(10)^2=400`

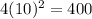
Surface area of new prism =
`4(8)^2=256`

`\Rightarrow k=(256)/(400)=(16)/(25)`

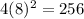
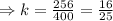
Hence, the scale factor =
`(16)/(25)`