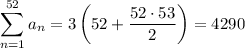The number of seats per row generate an arithmetic sequence. Let

denote the number of seats in the

-th row. We're told that the number of seats increases by 3 per row, so we can describe the number of seats in a given row recursively by
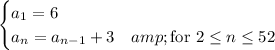
The total number of seats is given by the summation
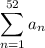
Because

is arithmetic, we can easily find an explicit rule for the sequence.
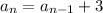

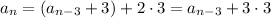

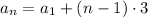
So the number of seats in the

-th row is exactly
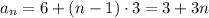
This means the total number of seats is
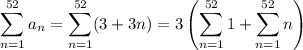
You should be familiar with the remaining sums. We end up with