I'll assume

is completely dominant over
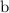
. Recall the Hardy-Weinberg equations:
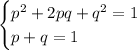
where
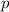
represents the allele frequency for brown fur, or the number of copies of the allele

within the population; and
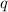
represents the allele frequency for white fur, or the number of copies of
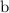
. In the first equation, the squared terms refer to the frequencies of the corresponding homozygous individuals, while
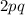
is the frequency of the heterozygotes.
We're told that 12 individual moles have white fur, so we know for sure that there are 12 homozygous recessive individuals, which means
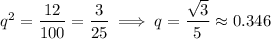
from which it follows that

Over time, H-W equilibrium guarantees that the allele frequencies

do not change within the population. For example, suppose we denote the frequency of the

allele in generation

by
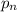
. Then
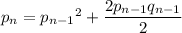
That is, the frequency

in the

-th generation has to match the frequency of

attributed to the
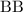
and half the
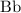
individuals of the previous generation.
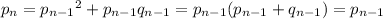
The same goes for
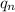
.