Question

What is the equation of a circle with its center at (0,-2) and passing through the point (3,-5)

Answer 1

Circle's Standard Form Equation:

`r^(2) = (x - xo)^(2) + (y - yo)^(2)`

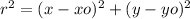
First you need to substitute the C (0,-2) in the equation, where: Xo = 0 and Yo = -2;


`r^(2) = (x - 0)^(2) + (y - ( -2))^(2) \\ r^(2) = x^(2) + (y + 2)^(2)`

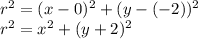
Now you substitute the Point (3,-5) values in the last expression, where: X = 3 and Y = -5;


`r^(2) = 3^(2) + (( - 5) + 2)^(2) \\ r ^(2) = 9 + ( - 3)^(2) \\ r^(2) = 9 + 9 \\ {r}^(2) = 18`

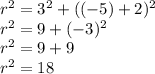
Now you get the R^2 value and substitute in the equation that you found putting the C values on it:


`r^(2) = x^(2) + (y + 2)^(2) \\ x^(2) + (y + 2)^(2) = 18`

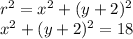
Here is your standard form equation of the circle.