Question

For the data set below, calculate the standard deviation to the nearest hundredth decimal place. 27 38 47 42 33 56 37 57 38 52

Answer 1

The standard deviation rounded to the nearest hundredth is 10.02.

Explanation:

The formula to find the standard deviation is

`\sigma = \sqrt^(2) )/(N-1)`

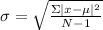
Where
`\mu` represents the mean,
`N` the total number of elements and
`x` is each element.

So, first we need to find the mean

`\mu =(\Sigma x)/(N)=(27+38+47+42+33+56+37+57+38+52)/(10)= 42.7`

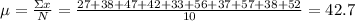
Then, we subtract the mean with each element and find its square power

`(27-42.7)^(2) =246.49\\(38-42.7)^(2)= 22.09\\(47-42.7)^(2)= 18.49\\(42-42.7)^(2)= 0.49\\(33-42.7)^(2)= 94.09\\(56-42.7)^(2)= 176.89\\(37-42.7)^(2)= 32.49\\(57-42.7)^(2)= 204.49\\(38-42.7)^(2)= 22.09\\(52-42.7)^(2)= 86.49`

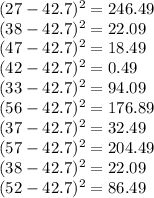
Then, we sum all, and that would be the numerator to find the standard deviation

`\sigma = \sqrt^(2) )/(N-1) =\sqrt{(904.1)/(9) } =√(100.46)\\ \sigma =10.02`

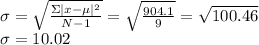
Therefore, the standard deviation rounded to the nearest hundredth is 10.02.

Answer 2

In order to calculate standard deviation, apply the standard deviation formula, which is given in the attached file. In this formula, we are finding the square root of the sum of the square of given values less their mean value (the sum of the given numbers divided to their amount) divided to N-1, where N is the amount of the given numbers. When we calculate the mean, it is 42.7 and the standard deviation is 10.02275