Question

Use graphs and tables to find the limit and identify any vertical asymptotes of the function.

Answer 1

Lim x→8- [1/(x-8)]=1/(8-8)=1/(-0)→Lim x→8- [1/(x-8)]=-Infinite

Vertical asymptote: x=8

Answer 2

The limit of the function is
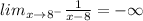`lim_(x\rightarrow 8^-)(1)/(x-8)=-\infty` and the vertical asymptotes is x=8.

Explanation:

The given function is

`f(x)=(1)/(x-8)`

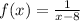
We need to find the value of

`lim_(x\rightarrow 8^-)(1)/(x-8)`

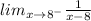
The graph of the function f(x) is attached below.

From the graph it is clear that the function approaches to -∞ as x approaches to 8 from left. So, by the graph we can say that

`lim_(x\rightarrow 8^-)(1)/(x-8)=-\infty`

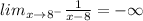
The table of values is attached below. From the table it is clear that the value of f(x) decreasing as the value of x is closed to 8 from left. So, by the table we can say that

`lim_(x\rightarrow 8^-)(1)/(x-8)=-\infty`

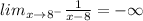
To find the vertical asymptotes equate denominator, equal to 0.

`x-8=0`

`x=8`

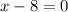
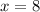
Therefore the limit of the function is
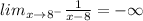`lim_(x\rightarrow 8^-)(1)/(x-8)=-\infty` and the vertical asymptotes is x=8.