Question

Consider the following sequence of numbers 3, -9, 27, -81, ….

Common Ratio Of The Sequence is?
A. 1/3
B. -1/3
C. -3
D. 3



The Sum Of The First Five Terms Of The Sequence Is?
A. 183
B. -303
C. -60
D. 363

Answer 1

QUESTION 1

The given sequence is
`3,-9,27,-81,...`.

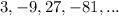The first term of the sequence is
`a_1=3`

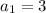
The second term is
`a_2=-9`

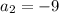
The common ratio can be found using any two consecutive terms of the sequence.

Thus, the common ratio is given by
`r=(a_n)/(a_(n-1))`.

This implies that,

`r=(-9)/(3)`

This simplifies to,

`r=-3`

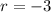
The correct answer is C

QUESTION 2

The sum of the first n terms of a geometric sequence is given by;

`S_n=(a_1(r^n-1))/(r-1)`.

Since we are looking for the first five terms, we substitute
`n=5`,
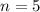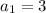`a_1=3` and
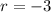`r=-3` into the formula to obtain,

`S_5=(3((-3)^5-1))/(-3-1)`

This will evaluate to give us;

`S_5=(3(-243-1))/(-3-1)`

`S_5=(3(-244))/(-4)`

`\Rightarrow S_5=3* 61`

`\Rightarrow S_5=183`

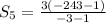
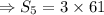
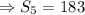
The correct answer is A