Question

Write parametric equations of the line 2x-y=3

Answer 1

In this item we are given with the equation, 2x - y = 3. The equation contains two variables, x and y. We assume in this item that the value of x is independent of the value of y; however, y values depends on the given values of x. In parametric form, the equation would take the form,

f(x) = y = ax + b

where a is the numerical coefficient of x and b is constant. Transforming the given equation to this form,

f(x) = y = 2x - 3

Answer 2

Answer: The required parametric equation is y=2t-3.

Explanation:

Since we have given that

2x+-y=3

We need to rewrite in parametric equation:

The parametric equation is written as

`f(x)=y=at+b`

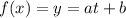
So, Arranging the given equation in the above equation, we get

`2x-y=3\\\\2x-3=y\\\\f(x)=y=2x-3`

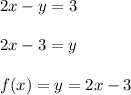
And then put x = t, to get the exact parametric form.

Hence, the required parametric equation is y=2t-3.