Question

How many mL of a 15% acid solution and how many mL of a 3% acid solution must be mixed to get 45 mL of a 7% acid solution?

Answer 1

15 mL of 15% acid solution and 30 mL of 3% acid solution

Step-by-step explanation:

The total number of moles of the mixture
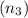`(n_(3))` is equivalent to the addition of the number of moles of the first solution
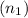`(n_(1))` and the number of moles of the second solution
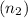`(n_(2))`. Mathematically,

`n_(1) +n_(2) = n_(3)`

`n_(1) = V_(1)*C_(1)`

`n_(2) = V_(2)*C_(2)`

`n_(3) = V_(3)*C_(3)`

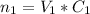
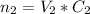
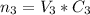
The volume of the mixture = 45 mL

The volume of first solution = x

The volume of second solution = 45 - x

Therefore:

0.15x + 0.03(45-x) = 0.07*45

0.15x + 1.35-0.03x = 3.15

0.12x = 1.8

x = 15

Thus, the volume of the first solution is 15 mL while the volume of the second solution is 30 mL.