Answer:
a) The orbital speed of a satellite with a orbital radius R (in meters) will have an orbital speed of approximately
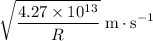 .
.
b) Again, if the orbital radius R is in meters, the orbital period of the satellite would be approximately
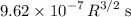 .
.
c) The orbital radius required would be approximately
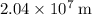 .
.
d) The escape velocity from the surface of that planet would be approximately
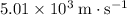 .
.
Step-by-step explanation:
a)
Since the orbit of this satellite is circular, it is undergoing a centripetal motion. The planet's gravitational attraction on the satellite would supply this centripetal force.
The magnitude of gravity between two point or spherical mass is equal to:
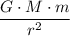 ,
,
where
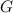 is the constant of universal gravitation.
is the constant of universal gravitation.
 is the mass of the first mass. (In this case, let
is the mass of the first mass. (In this case, let
 be the mass of the planet.)
be the mass of the planet.)
 is the mass of the second mass. (In this case, let
is the mass of the second mass. (In this case, let
 be the mass of the satellite.)
be the mass of the satellite.)
 is the distance between the center of mass of these two objects.
is the distance between the center of mass of these two objects.
On the other hand, the net force on an object in a centripetal motion should be:
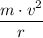 ,
,
where
 is the mass of the object (in this case, that's the mass of the satellite.)
is the mass of the object (in this case, that's the mass of the satellite.)
 is the orbital speed of the satellite.
is the orbital speed of the satellite.
 is the radius of the circular orbit.
is the radius of the circular orbit.
Assume that gravitational force is the only force on the satellite. The net force should be equal to the planet's gravitational attraction on the satellite. Equate the two expressions and solve for
 :
:
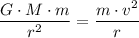 .
.
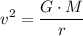 .
.
 .
.
Take
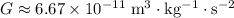 , Simplify the expression
, Simplify the expression
 :
:
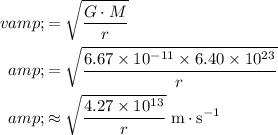 .
.
b)
Since the orbit is a circle of radius
 , the distance traveled in one period would be equal to the circumference of that circle,
, the distance traveled in one period would be equal to the circumference of that circle,
 .
.
Divide distance with speed to find the time required.
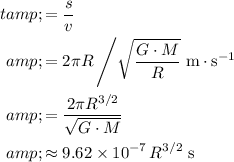 .
.
c)
Convert
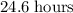 to seconds:
to seconds:
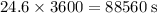
Solve the equation for
 :
:
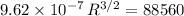 .
.
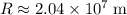 .
.
d)
If an object is at its escape speed, its kinetic energy (KE) plus its gravitational potential energy (GPE) should be equal to zero.
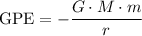 (Note the minus sign in front of the fraction. GPE should always be negative or zero.)
(Note the minus sign in front of the fraction. GPE should always be negative or zero.)
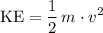 .
.
Solve for
 . The value of
. The value of
 shouldn't matter, for it would be eliminated from both sides of the equation.
shouldn't matter, for it would be eliminated from both sides of the equation.
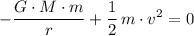 .
.
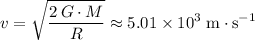 .
.