Question

Suppose you record 83 successes out of a random sample of 200 drawn from a population that yielded a proportion of successes of .40 in a previous study.

If you were to calculate a standardized test statistic for a hypothesis test about the population proportion, where H subscript 0 : p subscript 0 equals.40, what would your standard deviation of p with hat on top look like?

Answer 1

Answer: 0.0346

Explanation:

Required formula :
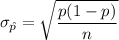`\sigma_{\hat{p}}=\sqrt{(p(1-p))/(n)}` , where p= population proportion

n= sample size.

Let p be the population proportion for successes .

As per given , we have

Null hypothesis :
`H_0: p_0=0.40`

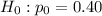
n= 200

Standard deviation of
`\hat{p}` =
`\sigma_{\hat{p}}=\sqrt{(0.40(1-0.40))/(200)}`

`\sigma_{\hat{p}}=√(0.0012)`

`\sigma_{\hat{p}}=0.0346410161514\approx0.0346`

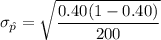
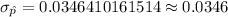
Hence , the required standard deviation of
`\hat{p}` = 0.0346