Question

n many population growth problems, there is an upper limit beyond which the population cannot grow. Many scientists agree that the earth will not support a population of more than 16 billion. There were 2 billion people on earth at the start of 1925 and 4 billion at the beginning of 1975. If yy is the population, measured in billions, tt years after 1925, an appropriate model is the differential equation

Answer 1

`(dP)/(dt) = rP(1 - (P)/(K)) = 0.017P(1 - (P)/(16))`

Explanation:

The logistic function of population growth, that is, the solution of the differential equation is as follows:

`P(t) = (KP_(0)e^(rt))/(K + P_(0)(e^(rt) - 1))`

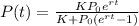
We use this equation to find the value of r.

In this problem, we have that:

`K = 16, P_(0) = 2, P(50) = 4`

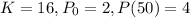
So we find the value of r.

`P(t) = (KP_(0)e^(rt))/(K + P_(0)(e^(rt) - 1))`

`4 = (16*2e^(50r))/(16 + 2*(e^(50r) - 1))`

`4 = (32e^(50r))/(14 + 2e^(50r))`

`56 + 8e^(50r) = 32e^(50r)}`

`24e^(50r) = 56`

`e^(50r) = 2.33`

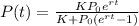
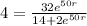
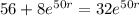
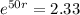
Applying ln to both sides of the equality

`50r = 0.8459`

`r = 0.017`

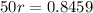
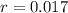
So

The differential equation is

`(dP)/(dt) = rP(1 - (P)/(K)) = 0.017P(1 - (P)/(16))`