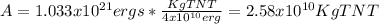Question

In 1945, the United States tested the world’s first atomic bomb in what was called the Trinity test. Following the test, images were published showing the evolution of the blast. A few years later, a British Scientist, by the name of G. I. Taylor, used dimensional analysis to predict the amount of energy released by the Trinity explosion, which was still classified information at the time. He did so, just by analyzing the images alone. He assumed the blast radius, R, depended only on the evolution time, t, the energy released, E, and the density of air, rho. Using the Buckingham-Pi theorem, find the dimensionless group, Π1 = k, where k is a constant. Assuming k = 1, find the energy released, in tons of TNT, if the radius of the blast wave at t = 0.025s is R = 140m. Take the density of air to be rho = 1.2kg/m3. Note, there are 4.184 × 109J per ton of TNT equivalent.

Answer 1

`r=K A^(1/5) \rho^(-1/5) t^(2/5)`

`A= (r^5 \rho)/(t^2)`

`A=1.033x10^(21) ergs *(Kg TNT)/(4x10^(10) erg)=2.58x10^(10) Kg TNT`

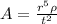
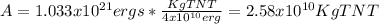
Step-by-step explanation:

Notation

In order to do the dimensional analysis we need to take in count that we need to conditions:

a) The energy A is released in a small place

b) The shock follows a spherical pattern

We can assume that the size of the explosion r is a function of the time t, and depends of A (energy), the time (t) and the density of the air is constant
`\rho_(air)`.

And now we can solve the dimensional problem. We assume that L is for the distance T for the time and M for the mass.

[r]=L with r representing the radius

[A]=
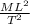`(ML^2)/(T^2)` A represent the energy and is defined as the mass times the velocity square, and the velocity is defined as
`(L)/(T)`

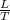
[t]=T represent the time

`[\rho]=(M)/(L^3)` represent the density.

Solution to the problem

And if we analyze the function for r we got this:

`[r]=L=[A]^x [\rho]^y [t]^z`

And if we replpace the formulas for each on we got:

`[r]=L =((ML^2)/(T^2))^x ((M)/(L^3))^y (T)^z`

And using algebra properties we can express this like that:

`[r]=L=M^(x+y) L^(2x-3y) T^(-2x+z)`

And on this case we can use the exponents to solve the values of x, y and z. We have the following system.

`x+y =0 , 2x-3y=1, -2x+z=0`

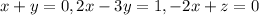
We can solve for x like this x=-y and replacing into quation 2 we got:

`2(-y)-3y = 1`

`-5y = 1`

`y= -(1)/(5)`

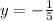
And then we can solve for x and we got:

`x = -y = -(-(1)/(5))=(1)/(5)`

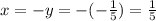
And if we solve for z we got:

`z=2x =2 (1)/(5)=(2)/(5)`

And now we can express the radius in terms of the dimensional analysis like this:

`r=K A^(1/5) \rho^(-1/5) t^(2/5)`

And K represent a constant in order to make the porportional relation and equality.

The problem says that we can assume the constant K=1.

And if we solve for the energy we got:

`A^(1/5)=(r)/(t^(2/5) \rho^(-1/5))`

`A= (r^5 \rho)/(t^2)`

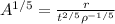
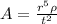
And now we can replace the values given. On this case t =0.025 s, the radius r =140 m, and the density is a constant assumed
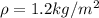`\rho =1.2 kg/m^2`, and replacing we got:

`A=(140^5 1.2 kg/m^3)/((0.025 s)^2)=1.033x10^(14) (kg m^2)/(s^2)`

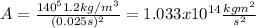
And we can convert this into ergs we got:

`A= 1.033x10^(14) (kgm^2)/(s^2) * (1 x10^7 egrs)/(1 (kgm^2)/(s^2))=1.033x10^(21) ergs`

And then we know that 1 g of TNT have
`4x10^4 erg`

And we got:

`A=1.033x10^(21) ergs *(Kg TNT)/(4x10^(10) erg)=2.58x10^(10) Kg TNT`