Question

Determine

whether b can be written as a linear
combination of a1 and a2. In other words, determine
whether weights x1 and x2 exist, such that x1a1 + x2a2 = b. Determine the
weights x1 and x2 if possible.
a1[4,5,-4]
a2[-4,3,3] b,[8,26,-10]

Answer 1

`<8,26,-10>=4.<4,5,-4>+2.<-4,3,3>`

Explanation:

Linear Combination Of Vectors

One vector
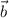`\vec b` is a linear combination of
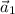`\vec a_1` and
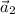`\vec a_2` if there are two scalars
`x_1, x_2` such as

`\vec b=x_1\vec a_1+x_2\vec a_2`

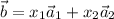
In our case, all the vectors are given in
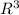`R^3` but there are only two possible components for the linear combination. This indicates that only two conditions can be used to determine both scalars, and the other condition must be satisfied once the scalars are found.

We have

`\vec a_1=<4,5,-4>,\ \vec a2=<-4,3,3>,\ \vec b=<8,26,-10>`

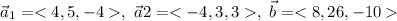
We set the equation

`<8,26,-10>=x_1.<4,5,-4>+x_2.<-4,3,3>`

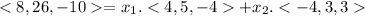
Multiplying both scalars by the vectors

`<8,26,-10>=<4x_1,5x_1,-4x_1>+<-4x_2,3x_2,3x_2>`

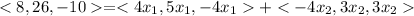
Equating each coordinate, we get

`4x_1-4x_2=8`

`5x_1+3x_2=26`

`-4x_1+3x_2=-10`

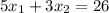
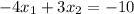
Adding the first and the third equations:

`-x_2=-2`

`x_2=2`

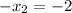
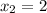
Replacing in the first equation

`4x_1-4(2)=8`

`4x_1=8+8`

`x_1=4`

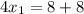
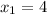
We must test if those values make the second equation become an identity

`5(4)+3(2)=20+6=26`

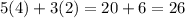
The second equation complies with the values of
`x_1` and
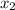`x_2`, so the solution is

`<8,26,-10>=4.<4,5,-4>+2.<-4,3,3>`