Question

Simplify your answer to the previous part and enter a differential equation in terms of the dependent variable xx satisfied by x=e5t. Enter the derivatives of xx using prime notation (x′,x′′,x′′′x′,x″,x‴).

Answer 1

x'-5x=0, or x''-25x=0, or x'''-125x=0

Explanation:

The function
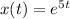`x(t)=e^(5t)` is infinitely differentiable, so it satisfies a infinite number of differential equations. The required answer depends on your previous part, so I will describe a general procedure to obtain the equations.

Using rules of differentiation, we obtain that
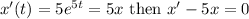`x'(t)=5e^(5t)=5x \text{ then }x'-5x=0`. Differentiate again to obtain,
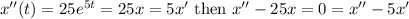`x''(t)=25e^(5t)=25x=5x' \text{ then }x''-25x=0=x''-5x'`. Repeating this process,
`x'''(t)=125e^(5t)=125x=25x' \text{ then }x'''-125x=0=x'''-25x'`.

This can repeated infinitely, so it is possible to obtain a differential equation of order n. The key is to differentiate the required number of times and write the equation in terms of x.